CAJITAS LIRO PARA RESOLVER PROBLEMAS ADITIVOS

 Las Cajitas Liro –  (PAEV) aditivos, sirven para resolver problemas aritméticos de Enunciado verbal, los estudiantes aprenderán a: 

• A resolver con autonomía y confianza los cuatro tipos de problemas aditivos (combinación, comparación, igualación y cambio o transformación) con resultados de hasta tres cifras.
• A canjear unidades, decenas y centenas con material estructurado.
• A formular problemas a partir de situaciones cotidianas y de sus conocimientos

CAPACIDADES A DESARROLLAR:

• Matematiza
• Comunica y Representa ideas matemáticas.
• Elabora y usa estrategias.
• Razona y Argumenta generando ideas matemáticas

DESCRIPCIÓN:

• 01 Caja didáctica rotulada con carteles identificadores de datos para problemas de combinación.
• 01 Caja didáctica rotulada con carteles identificadores de datos para problemas de cambio o transformación.
• 01 Caja didáctica rotulada con carteles identificadores de datos para problemas de comparación e igualación.
• 01 Cajita complementaria a la caja de comparación para ubicar la igualación de cantidades
• Ficha Técnica
• “X” de corospún (señalado de incógnita)

¿QUÉ MATERIALES VAMOS A UTILIZAR?

• Cajitas Liro para la resolución de problemas

Fichas, Cuentas, regletas o Material Base 10

ORIENTACIONES DIDÁCTICAS DE LAS  CAJITAS LIRO PARA RESOLVER PROBLEMAS ADITIVOS

 PARA RESOLVER  PROBLEMAS DE COMBINACIONES

Esta cajita se utiliza para resolver problemas de combinación en las que tenemos que juntar PARTE + PARTE para obtener un total. Ejemplo.

 

También nos ayuda a resolver los problemas en los que se proporcionan el  total (todo) y una de las partes. Ejemplo:

Juntamente con los niños, subrayamos e identificamos los datos, claramente debe identificarse que existe un total que está conformado por dos partes de las cuales sólo se nos proporciona una. Es un buen momento para explicar a los niños que combinando ambas partes, obtendremos el total completo, por eso a este tipo de problemas les llamamos problemas de combinación.

En las  cajitas liro paev aditivos, los niños colocan las fichas que corresponden al total y de ellas pasan las que corresponden a la 1º parte (que serían las de plástico). Hacer notar que lo que queda, corresponde a la 2º parte. Los niños graficarán lo que trabajaron y paralelamente pueden ir construyendo la sustracción para enlazar la manipulación del material concreto. Posteriormente, en la estructura del problema de  combinación  graficada en  papelote  (puede  ser  en el cuaderno)

CAJITAS LIRO PARA RESOLVER PROBLEMAS DE  IGUALACIÓN Y COMPARACIÓN

El punto de partida para trabajar los problemas de comparación e igualación es la comprensión e identificación de lo que se nos pide averiguar; esto lo lograremos a través de una detenida lectura del enunciado del problema (texto interrogativo) de tal manera que permita a los niños identificar los datos y entender que la pregunta nos pide comparar dichos datos y encontrar la diferencia entre ellos. Paso seguido, asignaremos una representación a cada una de estas cantidades estableciendo entre ellas una relación “mayor que” – “menor que”.

Comparación.

Pasaremos entonces a trabajar con la cajita de comparación colocando primero la cantidad menor en el lado respectivo, luego empezamos a colocar la cantidad mayor, pero, al momento de igualar las cantidades, marcamos la igualdad con la tableta separadora y el resto lo colocamos arriba, en el casillero marcado como “diferencia”, haciendo notar que lo colocado allí representa cuánto más tiene el mayor sobre el menor o cuánto menos tiene el menor  frente al mayor (según sea el caso).

Ejemplo:

¿En este caso, cómo asociamos el nivel concreto con el simbólico?

• Una forma sencilla es haciendo notar que si lo que nos piden es la diferencia, la única operación que nos da la diferencia es la resta, por lo tanto, cada vez que nos pidan comparar y encontrar la diferencia entre dos datos debemos restar.

Es importante remarcar desde los primeros contactos con la sustracción que el resultado es la “diferencia”; eso ayudará a los niños a asociar rápidamente la palabra diferencia con la sustracción.

• Otra manera es hacer ver que si al número mayor le quitamos la “igualdad” (señalada en la caja), nos quedamos con la diferencia. La acción de “quitar” nos da la idea de sustraer (es decir, restar).

Del mismo modo podemos proceder en el caso se nos pregunte “¿Cuántas muñecas menos que Fátima tiene Pierina? (Comparación 2). Fácilmente hallaremos la diferencia.

Veamos el siguiente problema

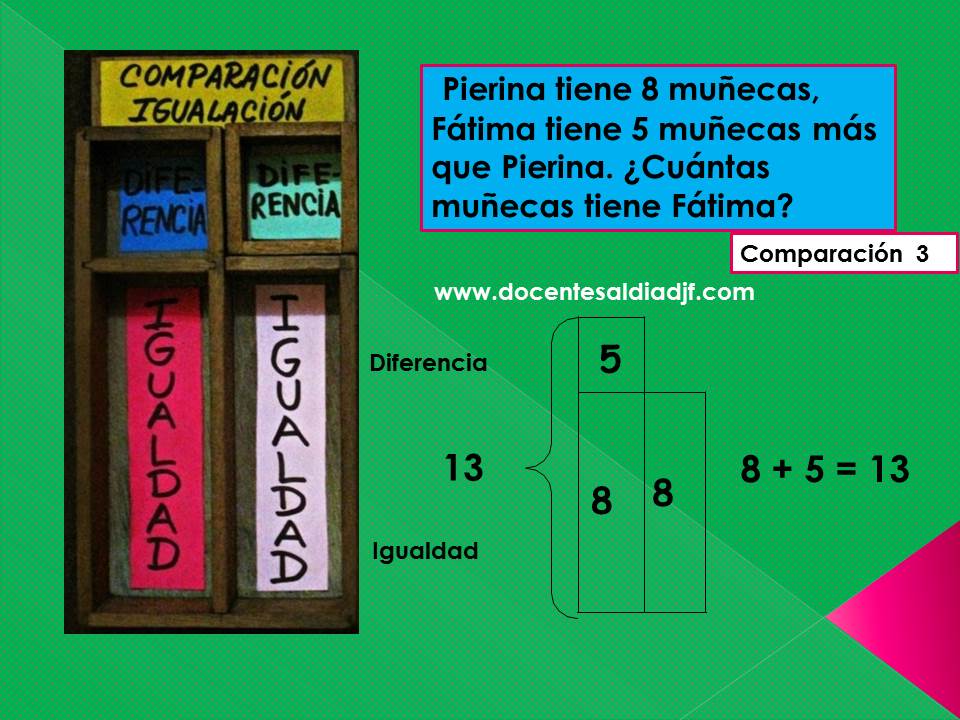
Primero hemos colocado las muñecas de Pierina en su casillero (empezar por la cantidad menor), luego las muñecas de Fátima incidiendo en que ella tiene 5 más (diferencia) además de las que tiene Pierina (igualdad). Finalmente, sumamos.

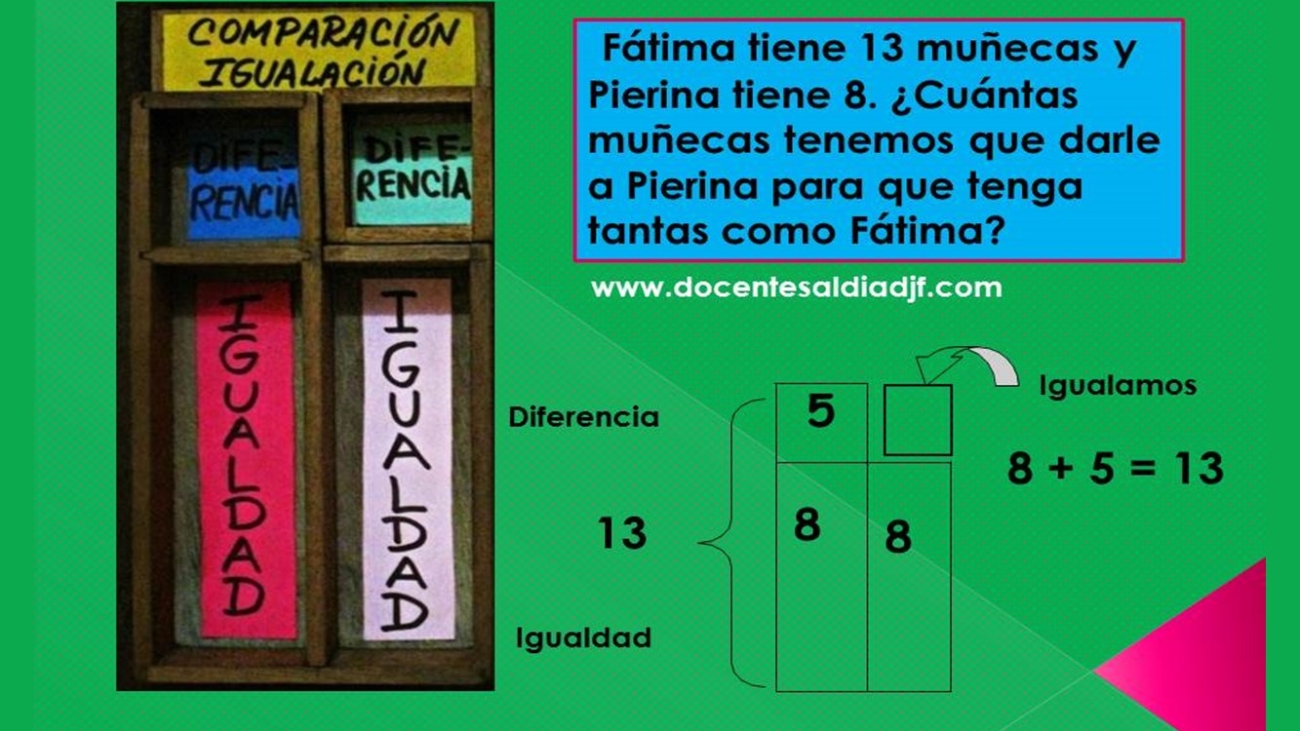
IGUALACIÓN

Son problemas en los que se nos pide averiguar cuánto le hace falta a uno  para igualar lo que tiene el otro. En ese caso, lo primero que debemos hallar es la diferencia y luego utilizando la cajita de igualación (anexa a la caja de comparación), igualamos con la diferencia hallada

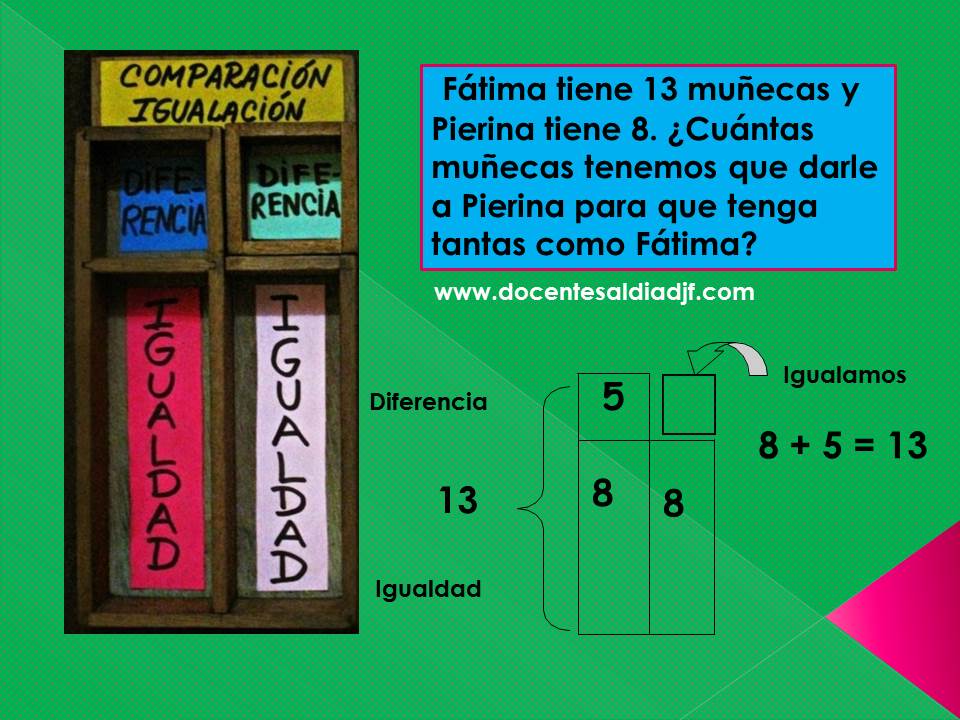
CAJITAS LIRO PARA RESOLVER PROBLEMAS DE CAMBIO.

En este caso diremos a los niños que se trata de problemas en los que habiendo una cantidad inicial, esta se transforma o cambia porque hay un aumento o una disminución de elementos, lo que da como resultado una nueva cantidad (final o después). Es importante que ellos aprendan a identificar estos datos (inicio, cambio, final). Se recomienda hacer algunos ejercicios de reconocimiento mediante la lectura de algunos problemas de cambio donde se irán reconociendo, identificando y subrayando los datos. Podemos también señalar cierta similitud con la estructura de un texto narrativo.

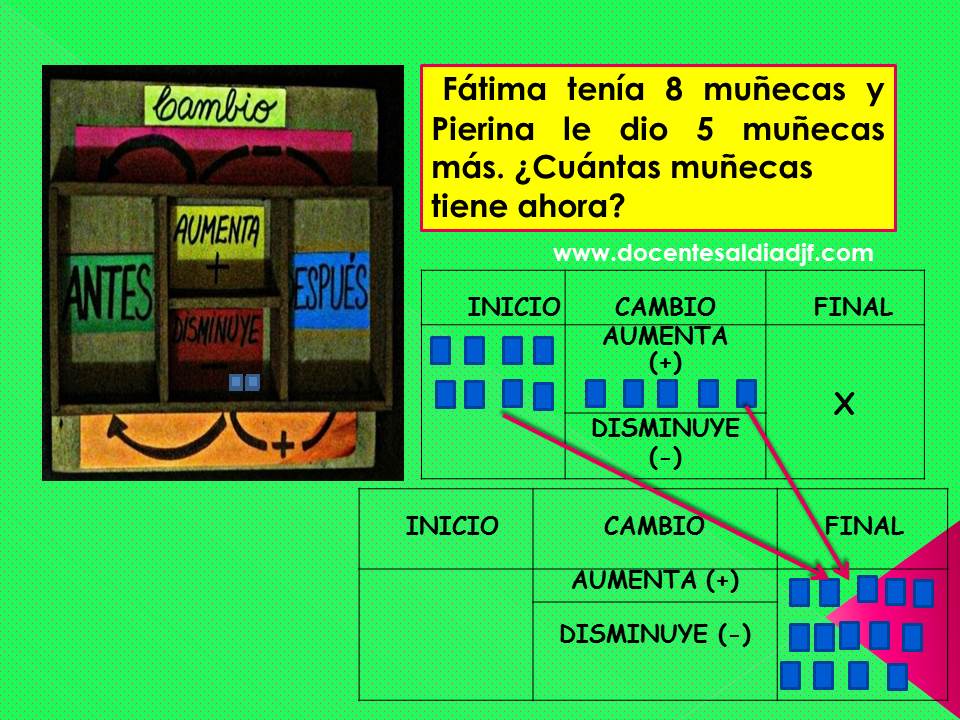
Pasaremos luego a los problemas de cambio 3 y 4, diremos a los niños que a veces la incógnita puede estar en la parte central, (cambio), ya sea aumentando o disminuyendo la cantidad inicial. Lo trabajamos así:

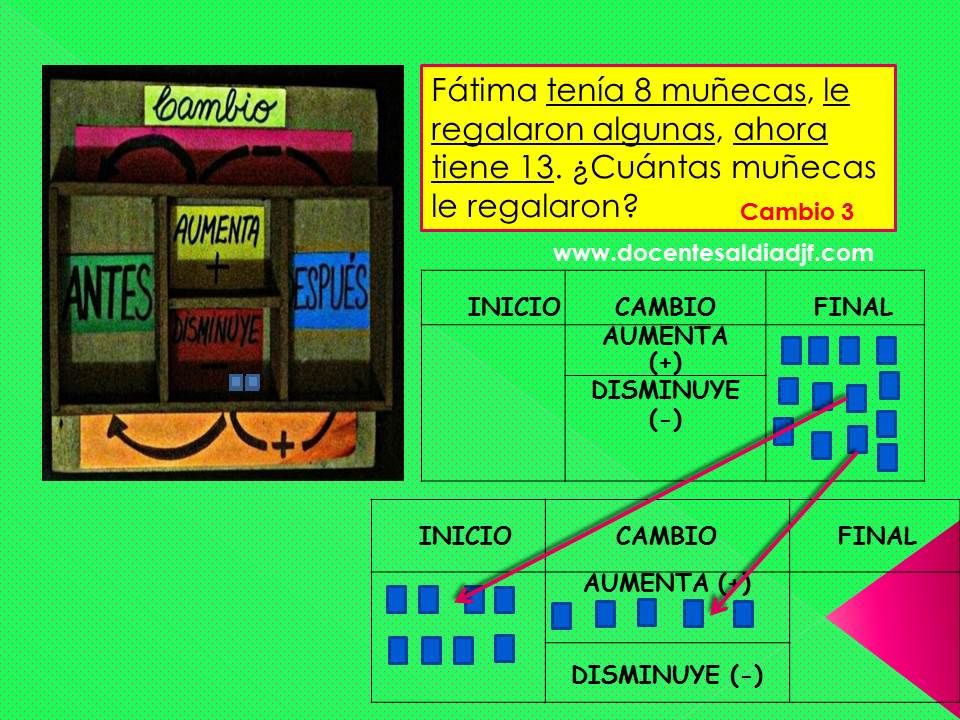
Podemos aplicar el método del cangrejo (vamos de atrás hacia adelante): Colocamos primero la cantidad del final y digo: “Al final Fátima tiene 13 muñecas, pero de estas 13, 8 son las que tenía al inicio, entonces las voy a regresar al inicio. Luego de retirar las 8 del inicio le quedan 5 y pregunto:

¿estas 5 a qué corresponden? Estas son las que le regalaron, por lo tanto las coloco en el casillero “aumenta”, entonces, ya descubrí cuántas son las que aumentaron, con lo cual queda despejada la “X”.

Debo llegar a la conclusión de que lo que hice es RESTARLE los 8 del inicio a los 13 del final, es decir,  convierto  todo  este  razonamiento  en  13  – 8  = 5  Es importante lograr este enlace entre el trabajo con material didáctico concreto (representación) con el procedimiento algorítmico (expresión simbólica).

• Resolviendo como ecuación tenemos: 8   +     X     =       13

X    =     13    –   8

X    =     5